TODO
定义
由于新手不太懂术语,规定行为一条数据,列为一组特征。 特征代表一列数据。如性别、年龄、身高等。 分类代表一个特征中不同的分类。如性别中分类为男女,天气中分类为晴、阴、雨、雪等,收入中分类为贫困、低收入、小康、中高收入者、富人等。
信息增益
引用自《机器学习实战》 >划分数据集的大原则:将无需的数据变得更加有序。我们可以使用多种方法划分数据集,但是每种方法都有各自的优缺点。组织杂乱无章数据的一种办法就是使用信息论度量信息,信息论是量化处理信息的分支学科。我们可以在划分数据之前或之后使用信息论量化度量信息的内容。 >在划分数据集之前之后信息发生的变化称为信息增益,知道如何计算信息增益,我们就可以计算每个特征值划分数据集获得的信息增益,获得信息增益最高的特征就是最好的选择。
节选 >集合信息的度量方式称为香农熵或者简称为熵,这个名字来源于信息论之父克劳德·香农。
下面这一段待修改,在进一步学习后发现有问题
如果不懂什么是信息增益(information)和熵(entropy)也无所谓,只需要知道熵越大则不确定性越大即可。因为我们需要的是不确定性小的特征,所以熵越小越好。试想决策树就是将信息一分为二,是不是最好某一个特征只有两种分类,如男、女。这样不确定性是极小的,因为它只能分为男和女。如果某一个特征有多个分类,如鸟类下有多种详细的分类,那么该特征的熵值就会很大,不确定性也很大。想想决策树就是将信息一分为二,我该选哪条线将鸟类一分为二?这是很难想的事情,所以这个特征并不好。以上只是举例,在具体项目中不一定对,并且决策树也不一定是二叉树(此处存疑?)。 熵的计算公式如下,其中pi是选择该分类的概率,即有20条数据,其中13条是男性,7条是女性。则男性的pi=13/20,女性的pi=7/20。 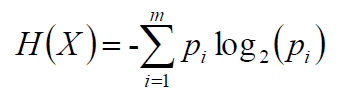
决策树构建步骤
决策树构建首先需要一个根结点,这是毋庸置疑的,但是根结点也不是一拍脑门就突然有了的。需要使用一些算法,现在一些常用的算法如:ID3(信息增益)、C4.5(信息增益率,解决ID3的问题,考虑自身熵)、CART(使用GINI系数来当做衡量标准,GINI系数和熵的衡量标准类似,但是计算方式不同)等。 以下使用ID3算法,给出如下训练数据,来源于唐宇迪机器学习视频中的截图。 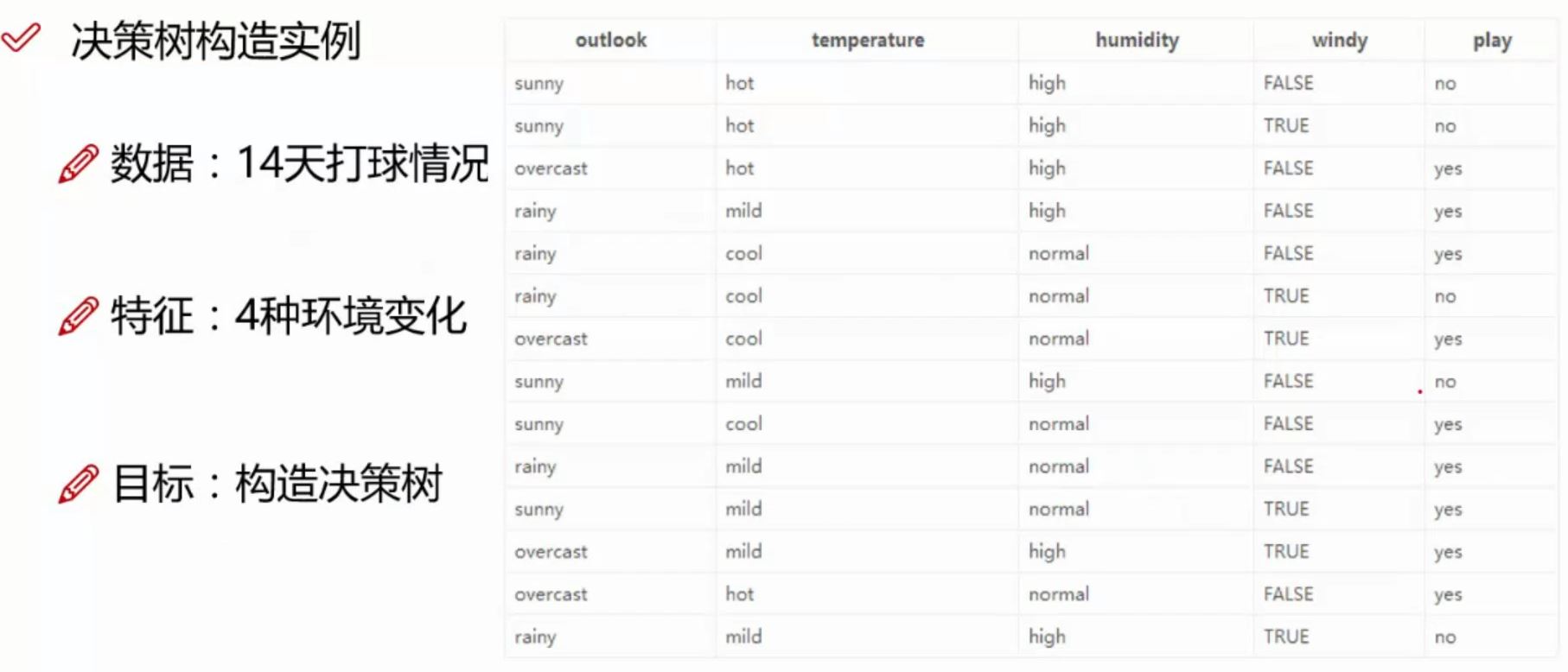 1. 首先计算全部数据的熵值,其实就是计算一下给出的数据中的最后一列(最后一列可以当做y)的熵值。
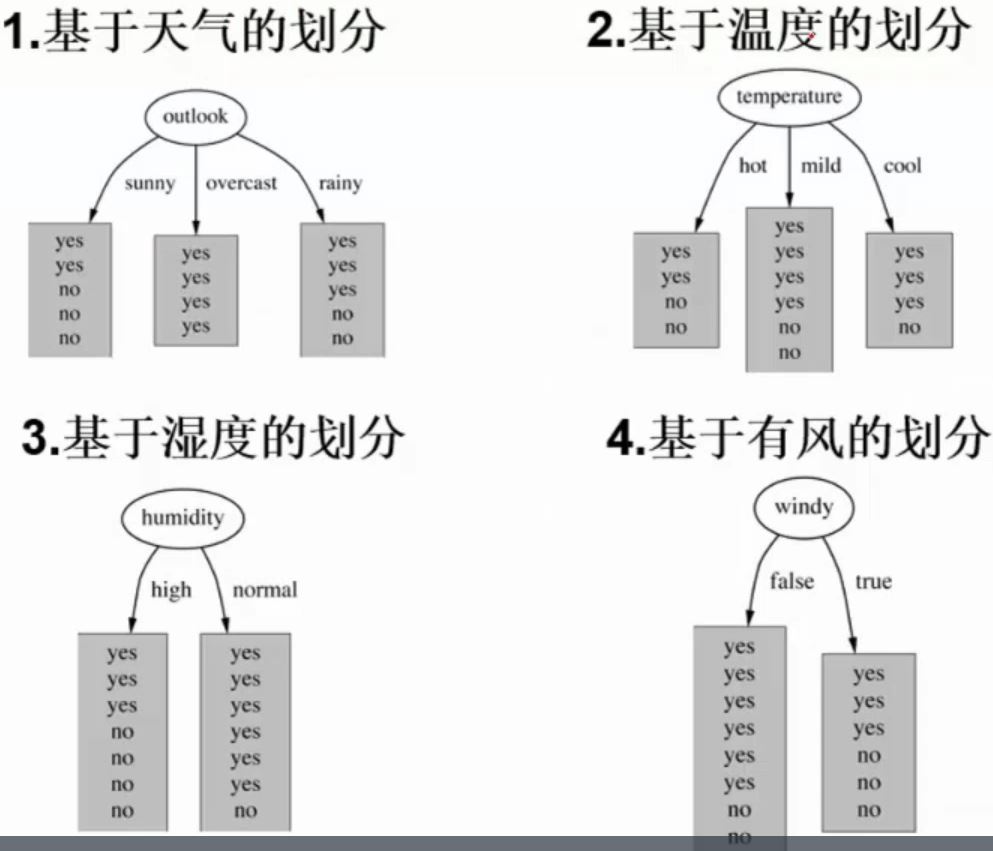
1. 首先计算全部数据的熵值,其实就是计算一下给出的数据中的最后一列(最后一列可以当做y)的熵值。  2. 计算其他特征的熵值。解释一下什么叫其他特征的熵值:比如 outlook 这个特征值,如果要计算它,首先需要知道 outlook 这个特征值分为 3 类,sunny、overcast 和 rainy,然后计算依次计算这三种类别的熵值。具体步骤是,比如计算 sunny 的熵值,那就将原数据中 outlook 不是 sunny 类别的数据全部删除,然后使用信息熵的公式计算剩余数据的熵值。其他的类别计算方式以此类推。计算完毕之后就得到了三个熵值,然后按照类别在特征中的比例相加即可。 如下图右侧,当天气为 sunny 时去打球的概率为\(\frac{2}{5}\),不去打球的概率为\(\frac{3}{5}\),利用上面的熵值公式计算结果为 0.971。再分别计算 outlook 其他分类:overcast 和 rainy 的熵值,此时得到了三个不同分类的熵值,即 sunny为\(\frac{5}{14}\), overcast为\(\frac{4}{14}\)。最终 outlook 的熵值即为\(\frac{5}{14} * 0.971 + \frac{4}{14} * 0 + \frac{5}{14} * 0.971 = 0.693\)。最后其他特征值也需要分别计算它们的分类的熵值。 这里可能会出现困惑,如果每个特征值都有多个分类,那计算量不是特别大?而且这里的分类是文字,计算量较小,如果分类是数字那么分类几乎不会重复,计算量不是突破天际?我在学决策树时出现了这种疑惑,后来发现算法确实是这样的,并没有错。 分类为文字称为离散值,分类为数值称为连续值。上面说到决策树碰到连续值计算量会非常大,解决办法:决策树连续值处理
2. 计算其他特征的熵值。解释一下什么叫其他特征的熵值:比如 outlook 这个特征值,如果要计算它,首先需要知道 outlook 这个特征值分为 3 类,sunny、overcast 和 rainy,然后计算依次计算这三种类别的熵值。具体步骤是,比如计算 sunny 的熵值,那就将原数据中 outlook 不是 sunny 类别的数据全部删除,然后使用信息熵的公式计算剩余数据的熵值。其他的类别计算方式以此类推。计算完毕之后就得到了三个熵值,然后按照类别在特征中的比例相加即可。 如下图右侧,当天气为 sunny 时去打球的概率为\(\frac{2}{5}\),不去打球的概率为\(\frac{3}{5}\),利用上面的熵值公式计算结果为 0.971。再分别计算 outlook 其他分类:overcast 和 rainy 的熵值,此时得到了三个不同分类的熵值,即 sunny为\(\frac{5}{14}\), overcast为\(\frac{4}{14}\)。最终 outlook 的熵值即为\(\frac{5}{14} * 0.971 + \frac{4}{14} * 0 + \frac{5}{14} * 0.971 = 0.693\)。最后其他特征值也需要分别计算它们的分类的熵值。 这里可能会出现困惑,如果每个特征值都有多个分类,那计算量不是特别大?而且这里的分类是文字,计算量较小,如果分类是数字那么分类几乎不会重复,计算量不是突破天际?我在学决策树时出现了这种疑惑,后来发现算法确实是这样的,并没有错。 分类为文字称为离散值,分类为数值称为连续值。上面说到决策树碰到连续值计算量会非常大,解决办法:决策树连续值处理 
 3. 通过1和2对比,选择出熵值最低的特征,并且熵值需要小于原始数据的基本熵值。 上述123步,均可以直接在choose_best_feature_index(dataset)函数中计算获得,顶多加几个封装过的函数,比如calculate_entropy(dataset),split_dataset(dataset, axis, value)等。 4. 删除已作出决策的数据,并将数据再次执行123步操作。 比如经过一轮筛选发现 outlook 为熵值最低的特征,则按照 outlook 的 3 个类别,决策树将会有 3 条分支,结点与结点连接的边上的值分别是 sunny、overcast 和 rainy。 首先按类别 sunny 继续往下决策,比如所有数据中,类别为 sunny 的数据全部为 yes,即想要出去打球,那么决策树递归结束。因为这个算法的目的就是要判断在这些特征下,这一天去打球是否合适,如果 sunny 下的每条数据都是 yes,就代表我们的目的已经达到了,也就没必要继续决策了。接下来假设类别 overcast 与 sunny 相反,那么就将类别是 overcast 的所有数据从原数据集中删去,再重复 123 步。 5. 构造决策树,决策树可以使用递归算法构建。 新手入门系列,完全可以仅使用python的dict来存储决策树。如:{'tearRate': {'reduced': 'no lenses', 'normal': {'astigmatic': {'no': {'age': {'young': 'soft', 'pre': 'soft', 'presbyopic': {'prescript': {'hyper': 'soft', 'myope': 'no lenses'}}}}, 'yes': {'prescript': {'hyper': {'age': {'young': 'hard', 'pre': 'no lenses', 'presbyopic': 'no lenses'}}, 'myope': 'hard'}}}}}}
3. 通过1和2对比,选择出熵值最低的特征,并且熵值需要小于原始数据的基本熵值。 上述123步,均可以直接在choose_best_feature_index(dataset)函数中计算获得,顶多加几个封装过的函数,比如calculate_entropy(dataset),split_dataset(dataset, axis, value)等。 4. 删除已作出决策的数据,并将数据再次执行123步操作。 比如经过一轮筛选发现 outlook 为熵值最低的特征,则按照 outlook 的 3 个类别,决策树将会有 3 条分支,结点与结点连接的边上的值分别是 sunny、overcast 和 rainy。 首先按类别 sunny 继续往下决策,比如所有数据中,类别为 sunny 的数据全部为 yes,即想要出去打球,那么决策树递归结束。因为这个算法的目的就是要判断在这些特征下,这一天去打球是否合适,如果 sunny 下的每条数据都是 yes,就代表我们的目的已经达到了,也就没必要继续决策了。接下来假设类别 overcast 与 sunny 相反,那么就将类别是 overcast 的所有数据从原数据集中删去,再重复 123 步。 5. 构造决策树,决策树可以使用递归算法构建。 新手入门系列,完全可以仅使用python的dict来存储决策树。如:{'tearRate': {'reduced': 'no lenses', 'normal': {'astigmatic': {'no': {'age': {'young': 'soft', 'pre': 'soft', 'presbyopic': {'prescript': {'hyper': 'soft', 'myope': 'no lenses'}}}}, 'yes': {'prescript': {'hyper': {'age': {'young': 'hard', 'pre': 'no lenses', 'presbyopic': 'no lenses'}}, 'myope': 'hard'}}}}}}
举一个简单的例子
这里有一个简单例子 运行结果: 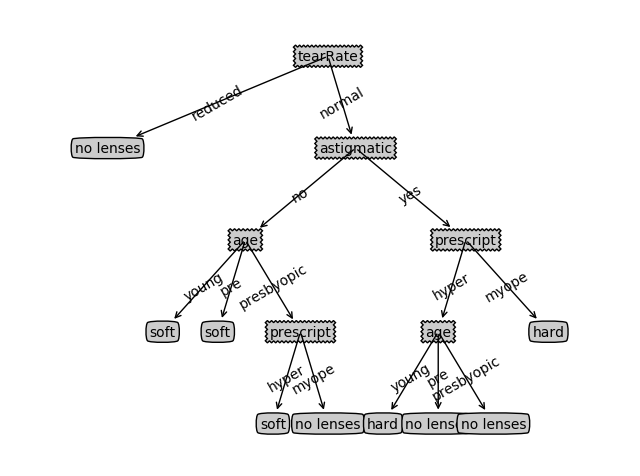
其他还未解决的问题
- 决策树处理缺失值
- 决策树处理连续值
- 剪枝的问题
