线性表
栈
只允许在表的一端就行插入和删除的线性表。栈分为顺序栈和链式栈,以下是它们各个操作的性能对比。
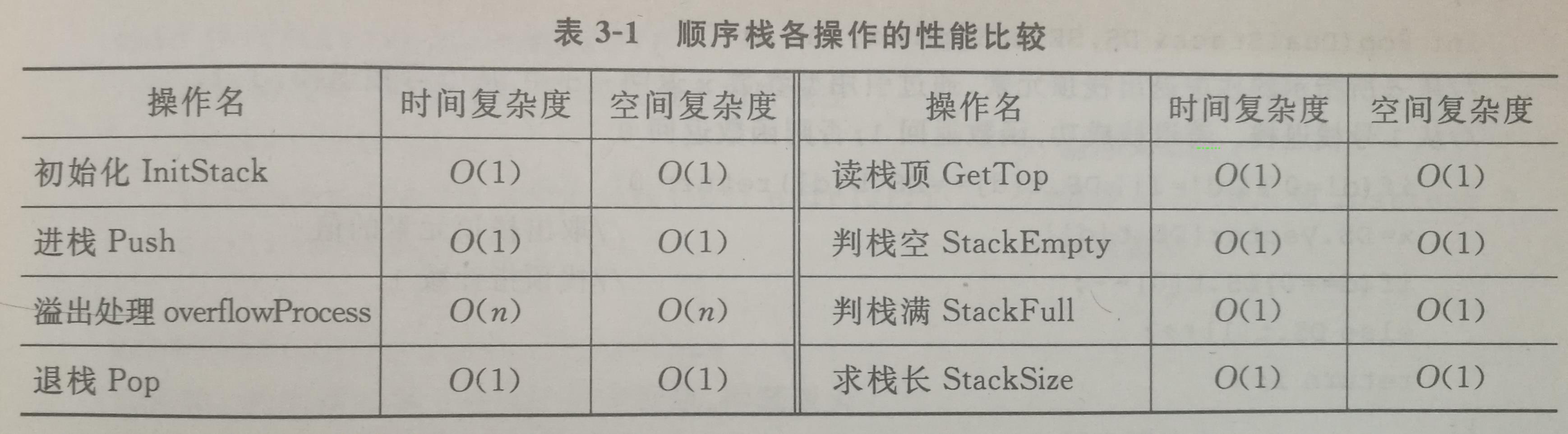
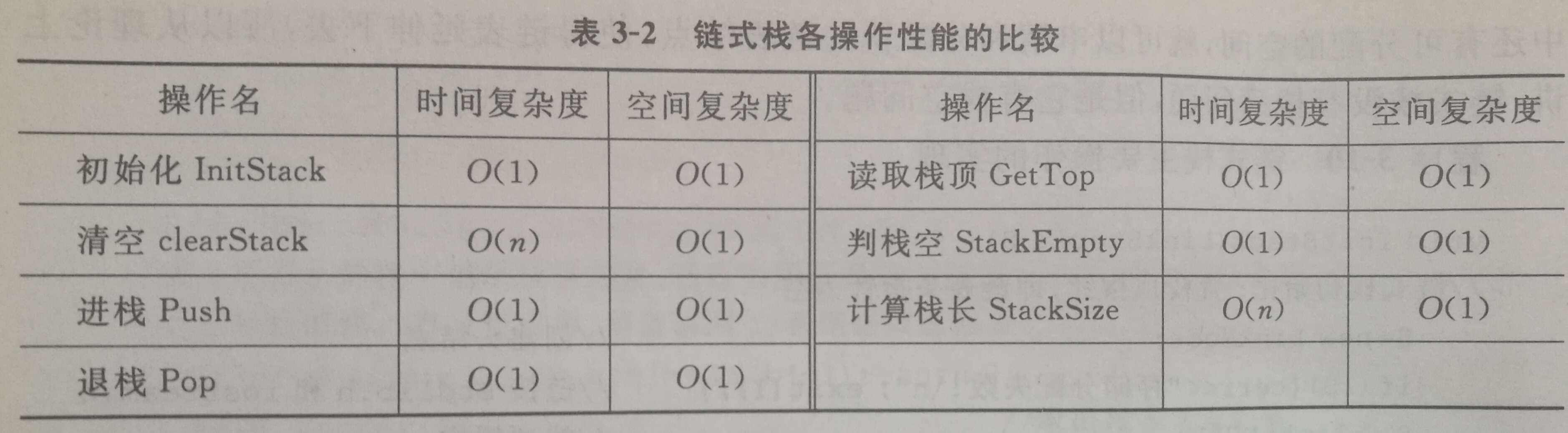
顺序栈
顺序栈指利用一块连续的存储单元作为栈元素的存储空间,只不过借用了数组来实现。设 n 为栈的最大容量,则栈可分为两种形式。
- 静态存储结构:预先申请或定义栈的存储空间,也就是说栈空间的容量有限。若栈满,会上溢。主要定义存储的数组以及当前top的索引位置。其他无关变量可自行定义,下同。
- 动态存储结构:如果栈满可自行扩充栈的大小,其中,原栈A中的内容会全部移植到新栈B。主要定义存储的数组、top的索引位置以及栈空间最大容量(maxCapacity)。其中,top 和 maxCapacity 可用来判断栈满栈空等。
链式栈
栈的链接存储表示。主要定义存储数据的变量以及链接下一个结点的变量。理论上链式栈没有栈满问题,但是它有栈空问题。如下图所示: 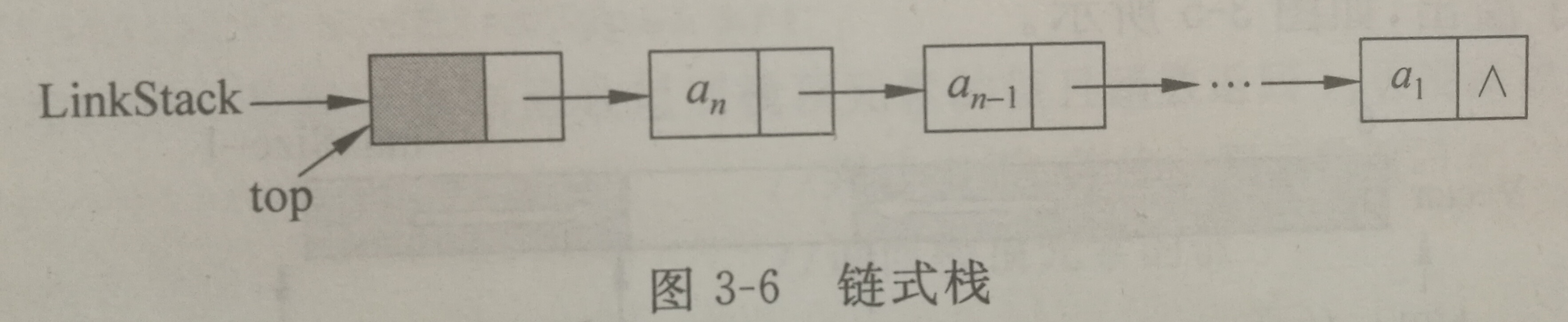
双栈
双栈共享同一个存储空间:栈0从头部存储,栈1从尾部开始存储,通过标志flag设置0,1等方法判断从头部开始存储还是尾部。两个栈共用一个栈空间,互相调剂,灵活性强。
栈的混洗
通过控制进栈和推栈的时机,可以得到不同的退栈序列。如进栈顺序为1,2,3,退栈序列有5种:{1,2,3},{1,3,2},{2,1,3},{2,3,1},{3,2,1}。注意{3,1,2}是不可能的退栈序列。其他数据元素于此类似。
栈的应用
- 数制转换
- 括号匹配
- 表达式的计算与优先级处理(一般使用后缀表达式计算表达式)
- 递归
队列
只允许在表的一端插入,在另一端删去。允许插入的一端叫队尾(rear),允许删除的一端叫做对头(front)。
顺序队列
就是队列的定义。主要定义存储数据的数组、rear 以及 front。它也会有溢出的情况:如图所示,数据A从上部进入,A被放在数组的0索引的位置。由于顺序队列是数组实现,所以当A出队列时,A后面的数据不会往前移动,因为如果移动那就要整体的往前移,太浪费时间了。所以当队列进满时,不管第一个数据前面还有没有空位置,都算溢出了。 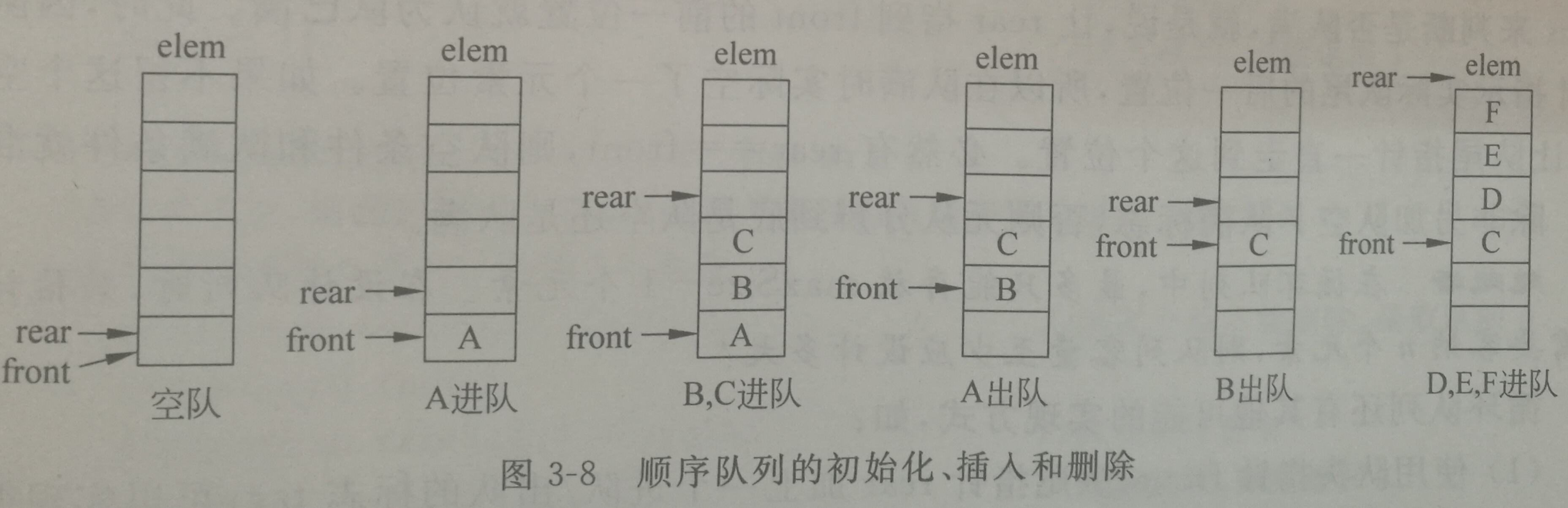
循环队列
解决了顺序队列的溢出问题。主要定义存储数据的数组、rear以及front。循环队列的首位相接,初始状态下,front和rear都指向0,但是当队列撑满时,rear指向的是front的前一格,这样用于区分是队空还是队满。可用取余(%)的计算方式前进1一格。 对头指针进 1:front = (front + 1) % maxSize; 对尾指针进 1:rear = (rear + 1) % maxSize; 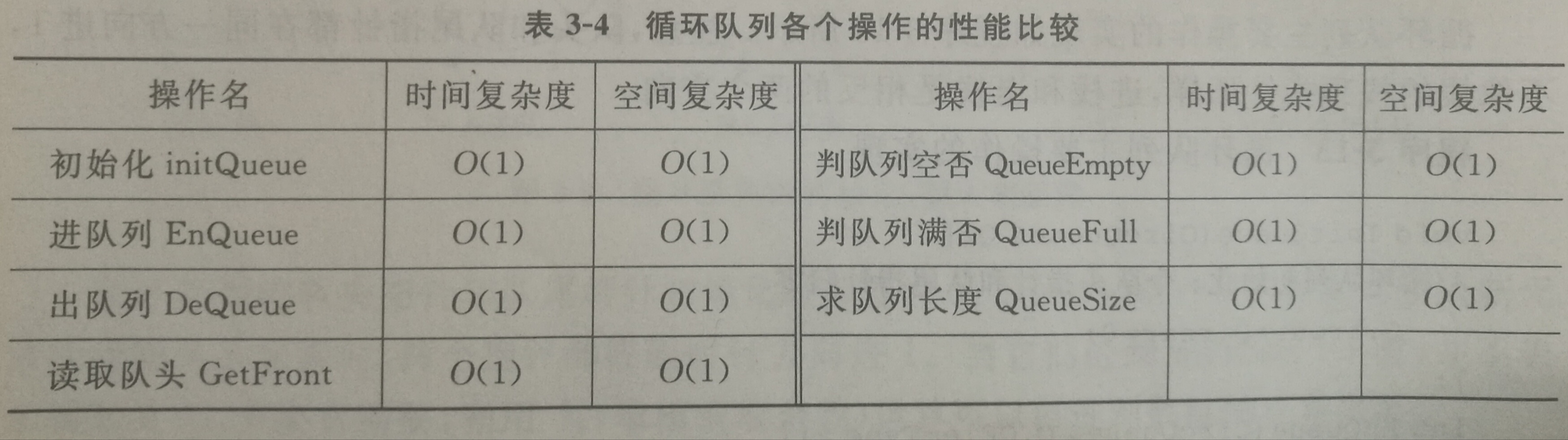
链式队列
基于单链表的队列。主要定义与单链表不同的是,插入和删除仅限于链表的两端。 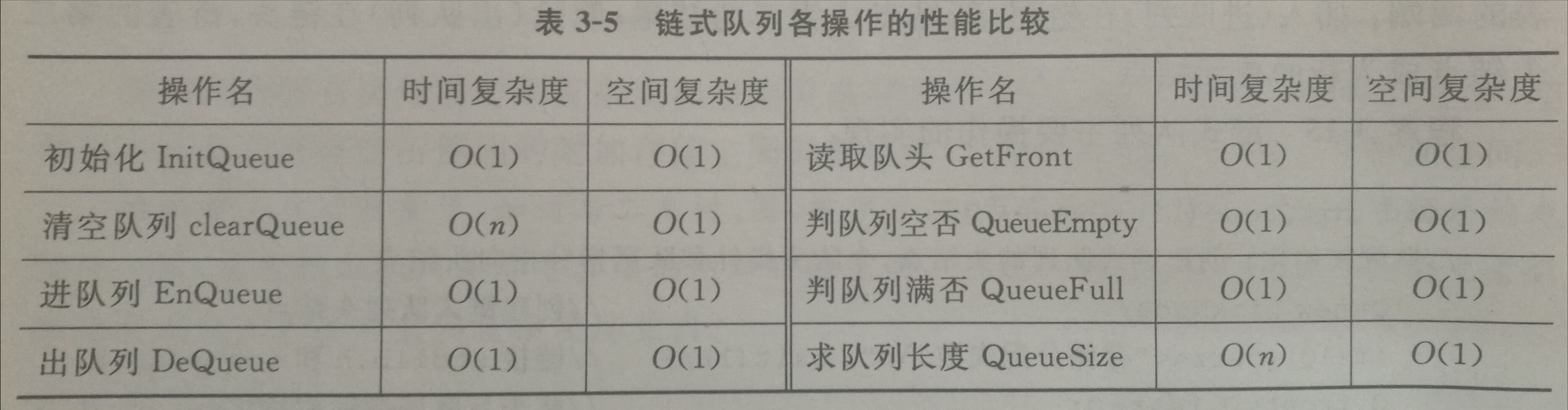
单循环队列
毫无意义,单链表本身所在的空间就不受限制。
队列的应用
打印杨辉三角与逐行处理
双端队列
杨辉三角:队列实现
下图为打印杨辉三角的文字说明。图片下面将对该文字进行进一步地解释: 
- 首先队列是从右往左看的(←),杨辉三角第一个数是1。int s,t。将1放入队尾
- 在生成第二行时,首先放入一个0.(放入0的步骤下面细讲)
- 令s=0,将1取出,令t=1.s+t=1放入0后面。
- 令s=t,将0取出令t=0. s+t=1放入1后面。
- 第二行生成完成。
- 在生成第三行时。也首先放入一个0.(放入的步骤下面细讲)
- 令s=0,将1取出,令t=1.s+t=1放入0后面
- 令s=t,将1取出令t=1. s+t=2放入1后面。
- 以此类推。
注:每生成一行之前都需要将s置为0;并且在队列尾部放入一个0,但是这里放一个0只是口头上表示的,实际写代码的时候,由于程序时线性执行的,电脑无法判断什么时候放0.所以需要写条件:当从队列中拿出一个0那么就代表一行生成完毕,所以当一个数与从队列中拿出的0相加时,就可以在队尾加一个0。下图是一个小型的演示。 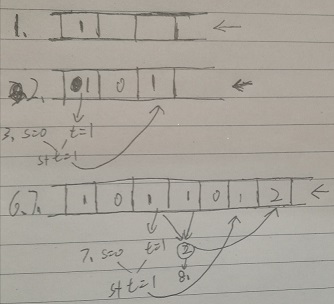
1 | /** |
