总结

返回所有可能解：递归时返回部分解或者初始化一个全局列表保存所有可能解
- 题 131 要求返回“解的所有可能”，那么在递归的时候势必需要返回部分解，最后拼装成全部解。或者可以初始化一个全局的列表用于保存解，但是我没这么做过。
返回所有可能解中的最优解：初始化一个全局列表保存所有可能解
- 题 1593 符合。但是并不需要真的保存所有解，尝试完一种情况后，删除即可。这样可以节省空间。
返回所有可能解中的任意解：初始化一个exit变量，当找到一个解时立即设置为True，并在其他的代码中加入判断，当且仅当exit==False时，程序才继续进行

算法思想

大白话：世界上有许多只能执行穷举法的问题，并且事实上，这些问题解决办法中不存在除穷尽搜索之外的方法。如果问题满足以下的描述就可以使用回溯法：算法从根结点开始枚举所有的解，深度优先。如果当前结点（可以是叶结点，也可以是非叶结点）的解不满足条件，则“回溯”返回，尝试上一个结点的其他子结点，即其他的可能解。直到找到一个可行解，或者找到所有可行解。可以将回溯法的搜索空间想象成一棵 n 叉树。

回溯法基本特征：

结点是用深度优先搜索的方法生成的；
不需要存储整棵搜索树（事实上，连树都没必要存储，只需要记录路径即可）

例子：三着色问题

给定一个无向图 G=(V, E)，需要使用三种颜色之一为 G 的顶点着色，使得没有两个相邻顶点的颜色相同。

合法：没有两个相邻顶点的颜色相同；
非法：相邻顶点的颜色相同；
搜索树：一个 n 个顶点的无向图共有 3^n 种可能的着色，所有可能的着色集合可以用一棵完全三叉树表示，即搜索树；
部分：如果某时没有两个相邻顶点的颜色相同，但图的着色还未完成，称此时的解为部分解；
现结点：当前待判断该着色是否合法的结点；
死结点：当前结点的着色已经是非法的，则称此结点为死结点。

面试题08.09. 括号/22. 括号生成

中等

class Solution:
    def generateParenthesis(self, n: int) -> List[str]:
        x = [-1 for _ in range(n * 2)]
        x[0] = 0
        result = []
        i = 1

        while i >= 0:
            while x[i] < 1:
                x[i] += 1
                if self.is_legal(x):
                    result.append(self.transform(x))
                elif self.is_partial(x, n):
                    i += 1
            x[i] = -1
            i -= 1
        return result

    def is_legal(self, x):
        """
        1）x 中最后一位不是 -1 才代表此种组合可能合法；
        2）约束函数的结果必须等于 0。（此方法无法保证括号是合法的，有部分组合可以使结果等于 0 也不合法，如“"()))(("”。
        这些组合出现的前提条件是使 is_partial() 为 True，当然，它们组合根本无法通过该方法，所以我们把合法判定的范围缩减了。）
        """
        return x[-1] != -1 and self.constraint(x) == 0

    def is_partial(self, x, n): 
        """
        1）x 中最后一位是 -1 才代表此种组合可能为部分；
        """
        return x[-1] == -1 and True if -n <= self.constraint(x) <= 0 else False

    def constraint(self, x):
        count = 0
        for item in x[::-1]:
            if item == 1:
                count += 1
            elif item == 0:
                count -= 1
            else:
                pass 
        return count

    def transform(self, x):
        pattern = []
        for item in x:
            if item == 0:
                pattern.append('(')
            elif item == 1:
                pattern.append(')')
            else:
                pattern.append('.')
        return ''.join(pattern)

17. 电话号码的字母组合

分析：回溯法模版套进去就行了。中等

class Solution:
    def letterCombinations(self, digits: str) -> List[str]:
        if len(digits) == 0:
            return []
        alpha_num_list = [3, 3, 3, 3, 3, 4, 3, 4]
        x = [-1 for _ in range(len(digits))]
        res = []
        i = 0
        while i >= 0:
            while x[i] < alpha_num_list[int(digits[i]) - 2] - 1:
                x[i] += 1
                if self.is_legal(x):
                    res.append(self.transform(x, alpha_num_list, digits))
                elif self.is_partial(x):
                    i += 1
            x[i] = -1
            i -= 1
        return res
                
    def is_legal(self, x):
        return x[-1] != -1
    
    def is_partial(self, x):
        return x[-1] == -1
    
    def transform(self, x, alpha_num_list, digits):
        res = []
        a = 97
        for i, item in enumerate(x):
            a += sum(alpha_num_list[: int(digits[i]) - 2])
            res.append(chr(a + item))
            a = 97
        return ''.join(res)

131. 分割回文串

中等

解题思路

画图。从字符串的第一个字符开始，将每种情况画出来，然后

假设字符串的长度为 1，则直接返回；
假设字符串的长度不为 1，但是其本身是回文，则加入部分解中；
否则进入循环，遍历所有的情况，每一种情况都要再进行递归；
1. 如果是字符串切割出的子字符串是回文，那么进行递归判断除子字符串之外的其他部分；
  1. 递归会产生一个部分解，将当前的回文子字符串加入每种部分解的开头。
2. 如果不是，那么不作任何处理；
返回部分解

class Solution:
    def partition(self, s: str) -> List[List[str]]:
        if len(s) == 1: return [[s]]

        solutions = []
        if self.is_huiwen(s): solutions.append([s])
        
        for pointer in range(1, len(s)):
            piece = s[: pointer]
            if self.is_huiwen(piece):
                partial_solutions = self.partition(s[pointer:])
                for partial_solution in partial_solutions:
                    partial_solution.insert(0, piece)
                solutions.extend(partial_solutions)
        return solutions
    
    def is_huiwen(self, s): return s == s[::-1]

306. 累加数

中等

解题思路

首先根据题目在脑子里思考搜索树应该是怎么样的，我的如下图所示（当然图中的例子，使用深度优先遍历就已经得到解了，其他的几个结点只是举个例子）：
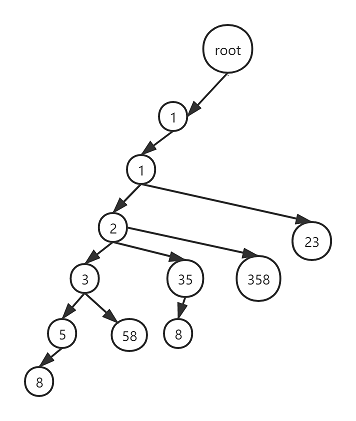
判断合法条件（合法即找到解）：
1. 字符串中的数字均考虑过，即已走到搜索树的叶结点
2. 符合约束函数：数字不得以“0”开头，“0”本身除外
3. 是否为累加的：前两个数字相加等于当前的数字
判断是部分解的条件（如果是部分解就进入下一层）：
1. 字符串中的数字未全考虑过，即未走到搜索树的叶结点
2. 同 2.2
3. 同 2.3

算法执行

字符串长度小于 3 直接返回 False
初始化前两个数字为 a, b = ''
开始递归，除了必需的变量，还需要一个字符串剩余长度（rest_len），方便在剩余的字符串中计算当前的数字
- 比如在上图中，当前所在层数为 3（即第四层），我们需要计算当前结点的数字。已知 rest_len = 3，str_len = 6，则取出当前结点的数字为 num[6 - 3: 6 - 3 + span]，span 为取数字的跨度，从 1 开始，所以就取到了数字“3”。在图中可以看到此层还有一个结点“35”，如果 span = 2，我们就取得了 num[6 - 3: 6 - 3 + 2]
  - array[i: j] 在 python 中意为取出在 array 中从 i 到 j 的元素（遵从包头不包尾原则）
- rest_len 另一个用途是计算 span，比如“112358”，rest_len = 3，那么我们只能选择取[3, 35 ,358]。我们从 1 遍历到 rest_len + 1，刚好可以得到可取的 span = [1, 2 ,3]
使用 rest_len 计算当前数字 c
合法则返回 True
部分则进入下一层
- 由于第 0 层和第 1 层无法进行比对，所以碰到此两层也可进入下一层

回溯法

class Solution:
    def __init__(self):
        self.success = False
        self.str_len = -1

    def isAdditiveNumber(self, num: str) -> bool:
        self.str_len = len(num)
        if self.str_len < 3:
            return False
        # 开始递归
        self.rec(num, self.str_len, 0, '', '')
        return self.success

    def rec(self, num_str, rest_len, current_layer, a, b):
        # 遍历所有可能的跨度
        for span in range(1, rest_len + 1):
            if not self.success:
                # 获取当前的数字
                start = self.str_len - rest_len
                c = num_str[start: start + span]
                # 是否合法，合法则找到解，直接退出程序
                if current_layer > 1 and self.is_legal(rest_len, span, a, b, c):
                    self.success = True
                    return
                # 是否为部分解，是则进入下一层
                elif current_layer <= 1 or self.is_partial(rest_len, span, a, b, c):
                    self.rec(num_str, rest_len - span, current_layer + 1, b, c)

    def is_legal(self, rest_len, span, a, b, c):
        return rest_len - span == 0 and self.constraint_func(a , b, c) and self.is_additive(a, b, c)

    def is_partial(self, rest_len, span, a, b, c):
        return rest_len - span != 0 and self.constraint_func(a , b, c) and self.is_additive(a, b, c)

    def constraint_func(self, a, b, c):
        return not (len(a) > 1 and int(a[0]) == 0 or len(b) > 1 and int(b[0]) == 0 or len(c) > 1 and int(c[0]) == 0)

    def is_additive(self, a, b, c):
        return int(a) + int(b) == int(c)

842. 将数组拆分为斐波那契序列

中等

解题思路

本代码最后没有通过测试，但是我验算了最后打印出来的错误提示，发现并没有错。后来发现其他人也有遇到这问题，所以暂时不做这题了。

import copy


class Solution:
    def __init__(self, ):
        self.exit = False
        self.solution = None

    def splitIntoFibonacci(self, S: str) -> List[int]:
        if len(S) < 3:
            return []
        
        def f(start): 
            if self.done(solution, S, start):
                self.exit = True
                self.solution = copy.copy(solution)
            elif self.partial(solution, S, start):
                for end in range(start + 1, len(S) + 1):
                    piece = S[start: end]
                    if int(piece[0]) == 0 and len(piece) > 1:
                        break 
                    solution.append(int(piece))
                    f(end)
                    solution.pop()
            
        solution = []
        f(0)
        return self.solution
    
    def is_fibonacci(self, solution):
        for i in range(2, len(solution)):
            if solution[i - 2] + solution[i - 1] != solution[i]:
                return False
        return True
    
    def done(self, solution, S, start):
        return len(solution) >= 3 and self.is_fibonacci(solution) and start >= len(S)
    
    def partial(self, solution, S, start):
        return len(solution) < 3 or (self.is_fibonacci(solution) and start < len(S) and not self.exit)

1219. 黄金矿工

中等

解题思路

尝试网格中的所有位置，如果该位置上黄金为零则跳过，否则计算可以挖掘最多黄金的数量；
如果已经挖掘完毕，则返回黄金数量；
否则前进一格，具体为“上下左右”四个方向；
1. 如果前进一格之后的位置，是一个无效位置，则跳过；
2. 否则递归；
3. 计算走“上下左右”四个方向上，黄金数量最多的那个方向。注：我们只需要黄金的数量即可，并不需要记录路径。

class Solution:
    def getMaximumGold(self, grid: List[List[int]]) -> int:
        max_gold = 0
        for which_row, row in enumerate(grid):
            for which_column, gold in enumerate(row):
                if gold == 0:
                    continue
                solution = [[0 for _ in row] for row in grid]
                total_gold = self.getMaximumGold_(solution, grid, (which_row, which_column))
                if total_gold > max_gold: max_gold = total_gold
        return max_gold
    
    def getMaximumGold_(self, solution, grid, pos):
        i, j = pos[0], pos[1]
        gold = grid[i][j]
        solution[i][j] += 1

        max_gold = gold
        if self.done(solution, grid, i, j):
            return gold
        else:
            for offset_i, offset_j in [(-1, 0), (1, 0), (0, -1), (0, 1)]:
                new_i, new_j = i + offset_i, j + offset_j
                if not (0 <= new_i < len(grid) and 0 <= new_j < len(grid[0])) or solution[new_i][new_j] == 1 or grid[new_i][new_j] == 0:
                    continue
                partial_gold = self.getMaximumGold_(solution, grid, (new_i, new_j))
                solution[new_i][new_j] -= 1

                if max_gold < gold + partial_gold: max_gold = gold + partial_gold
        return max_gold

    def done(self, solution, grid, i, j):
        for offset_i, offset_j in [(-1, 0), (1, 0), (0, -1), (0, 1)]:
            new_i, new_j = i + offset_i, j + offset_j
            if 0 <= new_i < len(grid) and 0 <= new_j < len(grid[0]):
                if grid[new_i][new_j] > 0 and solution[new_i][new_j] == 0:
                    return False
        return True

1593. 拆分字符串使唯一子字符串的数目最大

class Solution:
    def __init__(self, ):
        self.max_num = -1
        self.solution = []

    def maxUniqueSplit(self, s: str) -> int:
        self.maxUniqueSplit_(s, 0)
        return self.max_num
    
    def maxUniqueSplit_(self, s, i):
        if self.done(s, i):
            self.max_num = max(self.max_num, len(self.solution))
        elif self.partial(s, i):
            for j in range(i + 1, len(s) + 1):
                piece = s[i: j]
                if piece not in self.solution:
                    self.solution.append(piece)
                    self.maxUniqueSplit_(s, j)
                    self.solution.pop()
    
    def done(self, s, i): return len(s) <= i

    def partial(self, s, i): return len(s) > i

面试题 08.07. 无重复字符串的排列组合

中等

解题思路

挺简单的，就是一个全排列。

class Solution:
    def permutation(self, S: str) -> List[str]:
        if len(S) == 1: return [S]
        
        solutions = []
        for i in range(len(S)):
            partial_permutation = self.permutation(S[: i] + S[i + 1:])
            for pp in partial_permutation:
                solutions.append(S[i] + pp)
        return solutions

博客

【算法设计题目】回溯法

总结

算法思想

例子：三着色问题

面试题08.09. 括号/22. 括号生成

17. 电话号码的字母组合

131. 分割回文串

解题思路

306. 累加数

解题思路

算法执行

回溯法

842. 将数组拆分为斐波那契序列

解题思路

1219. 黄金矿工

解题思路

1593. 拆分字符串使唯一子字符串的数目最大

面试题 08.07. 无重复字符串的排列组合

解题思路